Der Kurs startet mit den verschiedenen Lösungsverfahren für lineare Gleichungssysteme. Ausgehend von der Wiederholung der klassischen Mittelstufenverfahren Gleichsetzungsverfahren, Additionsverfahren und Einsetzungsverfahren wird sowohl das Gauß-Jordan-Verfahren als auch das Determinantenverfahren eingeführt. Es folgen die Rechengesetze zur Matrizenrechnung sowie die Bestimmung der Inversen von quadratischen Matrizen.
Dann folgt der eigentliche Einstieg in die Analytische Geometrie mit dem Begriff des Vektors in den Dimensionen 1, 2 und 3 mit den dazugehörigen Operationen inklusive Skalar- und Vektorprodukt.
Nach den Erweiterungen zu den Konfidenzintervallen wird es um den Wahrscheinlichkeitsbegriff gehen. Dabei werden Permutationen und die zwei wichtigen Urnenmodelle Urne 1 und Urne 2 eingeführt. Aufbauend auf dem Urnenmodell 2 wird dann die Binomialverteilung untersucht sowie der Erwartungswert und die Standardabweichung hergeleitet. Anwendung findet dann die Binomialverteilung in den Prognoseintervallen. Bedingte Wahrscheinlichkeiten und Markowketten sind zusätzlich eingebundene Lerninhalte. Zum Abschluss wird es eine Vertiefung der analytischen Geometrie in der Ebene geben, die im 1. Kurssemester nur vorbereitend für die lineare Algebra behandelt wurde.
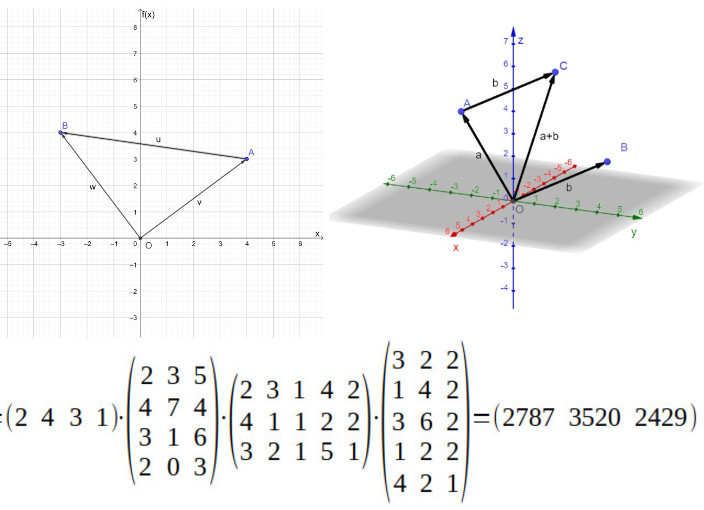
Am Beispiel des 2- und 3-dimensionalen Raumes wird der Vektorbegriff und seine Rechenstruktur erarbeitet. Die Anwendung dieser Rechenstruktur findet ihre Fortsetzung in der Matrizenrechnung, die als Werkzeug für Materialverpflechtung und Leontief-Modell in der Wirtschaft eine bedeutende Rolle spielt. Der Kurs endet mit Markow-Ketten, die auch in der Stochastik eine Bedeutung haben.
- Manager:in: Harald Rothkirch
